PLS - AGENCIAS
Roberto Gil-Saura
2022-04-24 20:07:28
NOTA: Incluye constructo de segundo orden
1 Tablas muestra
2 Modelización
El modelo de medida es el siguiente:
Modelo de medida
El modelo estructural es el siguiente:
Modelo estructural
2.1 Análisis de la fiabilidad
Para el modelo de medida se han considerado composites, mode A (reflectivos???). De este modo, el primer paso debe ser observar el resumen de los indicadores de fiabilidad, consistencia interna y validez.
El resultado del análisis muestra todas las escalas que apoyan las variables latentes tienen un Cronbach’s alpha mayor que 0.7, completado por una fiabilidad del compuesto rhoC también por encima de 0.7. para valores superiores a 0.91.
alpha rhoC AVE rhoA
VCC 0.829 0.864 0.523 0.881
RQ 0.795 0.879 0.708 0.803
ECOSAT 0.789 0.880 0.714 0.830
Alpha, rhoC, and rhoA should exceed 0.7 while AVE should exceed 0.52.2 Validez convergente
2.2.1 AVE
Del mismo modo, para evaluar la validez convergente o grado con el que una medida correlaciona positivamente con medidas alternativas del mismo constructo, usamos el coeficiente AVE (average variance extracted) que también cumple con la expectativa de estar por encima de 0.5.
alpha rhoC AVE rhoA
VCC 0.829 0.864 0.523 0.881
RQ 0.795 0.879 0.708 0.803
ECOSAT 0.789 0.880 0.714 0.830
Alpha, rhoC, and rhoA should exceed 0.7 while AVE should exceed 0.5Los indicadores son mostrados de forma conjunta en el siguiente gráfico.
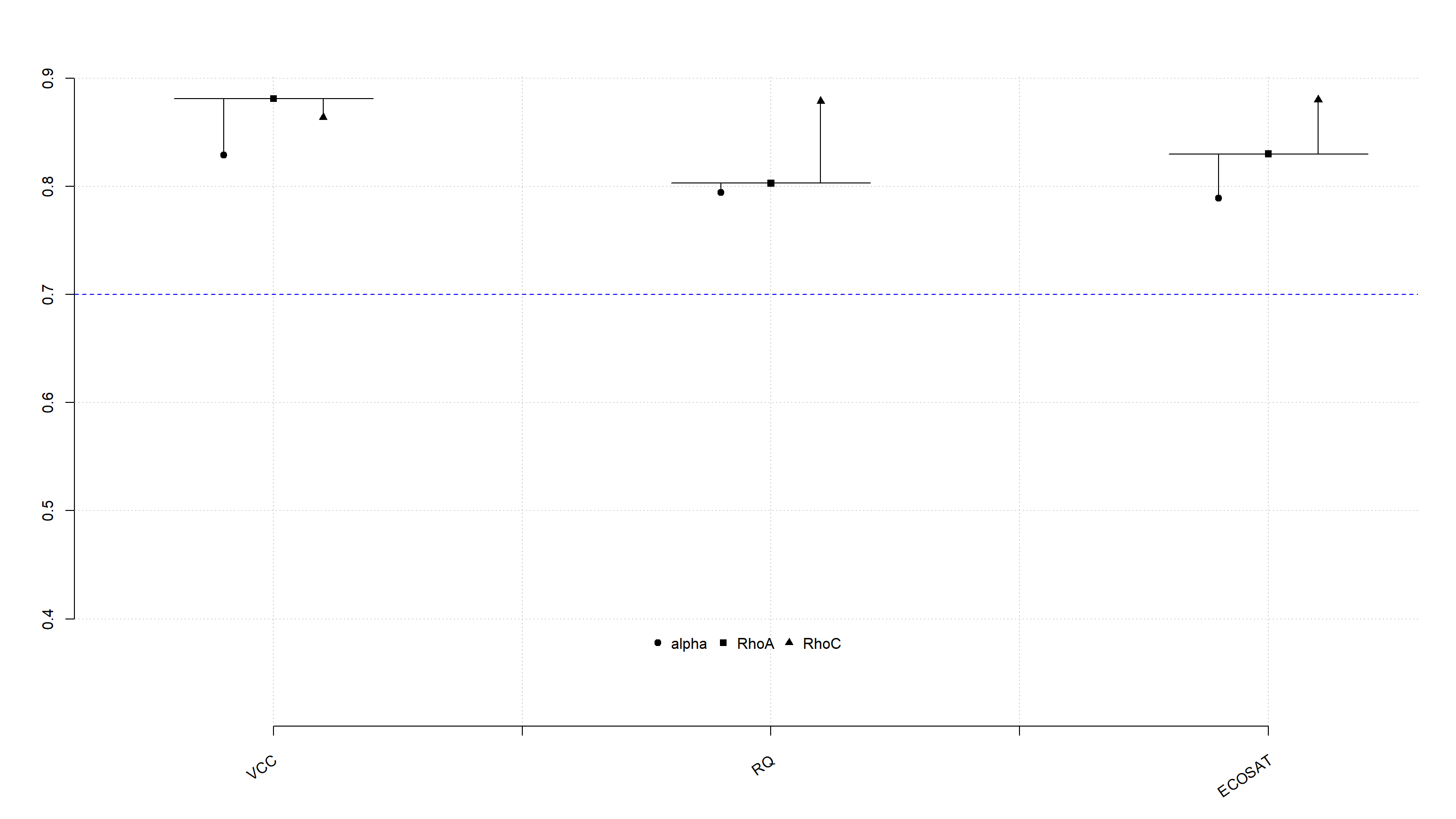
Tabla de fiabilidad
2.2.2 Análisis de las cargas
Por otro lado, es importante analizar también las cargas o loadings, indicadores de la fiabilidad del indicador en el constructo, y que deberían ser mayores de 0.7 para retener el indicador; para aquellas que están entre 0.4 y 0.7 debe ser analizado el comportamiento del constructo ante una eliminación del indicador con carga baja2.
VCC RQ ECOSAT TRUST COMMIT SOCSAT
VCC1 0.794 0.000 0.000 0.000 0.000 0.000
VCC2 0.831 0.000 0.000 0.000 0.000 0.000
VCC3 0.635 0.000 0.000 0.000 0.000 0.000
VCC4 0.865 0.000 0.000 0.000 0.000 0.000
VCC5 0.674 0.000 0.000 0.000 0.000 0.000
VCC6 0.462 0.000 -0.000 0.000 0.000 0.000
TRUST 0.000 0.820 0.000 0.000 0.000 0.000
COMMIT 0.000 0.855 0.000 0.000 0.000 0.000
SOCSAT 0.000 0.848 0.000 0.000 0.000 0.000
ECOSAT1 0.000 0.000 0.934 0.000 0.000 0.000
ECOSAT2 0.000 0.000 0.916 0.000 0.000 0.000
ECOSAT3 0.000 0.000 0.657 0.000 0.000 0.000
TRUST1 0.000 0.000 0.000 0.935 0.000 0.000
TRUST2 0.000 0.000 0.000 0.832 0.000 0.000
TRUST3 0.000 0.000 0.000 0.846 0.000 0.000
COMMIT1 0.000 0.000 0.000 0.000 0.885 0.000
COMMIT2 0.000 0.000 0.000 0.000 0.909 0.000
COMMIT3 0.000 0.000 0.000 0.000 0.816 0.000
COMMIT4 0.000 0.000 0.000 0.000 0.859 0.000
SOCSAT1 0.000 0.000 0.000 0.000 0.000 0.769
SOCSAT2 0.000 0.000 0.000 0.000 0.000 0.922
SOCSAT3 0.000 0.000 0.000 0.000 0.000 0.9002.3 Validez discriminante
2.3.1 Cross-loadings
Para el análisis de la validez discriminante o capacidad de un constructo de ser realmente distinto a otros, utilizamos las denominadas cross-loadings, que miden esa capacidad del constructo. En la tabla adjunta se puede observar en cada indicador carga de forma superior en su variable latente, siendo el resto de cargas de menor intensidad.
VCC RQ ECOSAT
VCC1 0.794 0.564 0.616
VCC2 0.831 0.496 0.548
VCC3 0.635 0.246 0.085
VCC4 0.865 0.529 0.436
VCC5 0.674 0.255 0.090
VCC6 0.462 0.203 -0.057
TRUST 0.385 0.820 0.526
COMMIT 0.584 0.855 0.504
SOCSAT 0.485 0.848 0.671
ECOSAT1 0.422 0.617 0.934
ECOSAT2 0.432 0.635 0.916
ECOSAT3 0.451 0.452 0.6572.3.2 Fornell-Larcker
El criterio de Fornell-Larcker, compara la raíz cuadrado del AVE con la correlación de las variables latentes. La raíz cuadrada del AVE de cada constructo, debería ser más grande que la más alta correlación con cualquier otro constructo. Se puede observar en la tabla siguiente que el valor en la diagonal principal, es mayor que el resto de valores en la parte inferior de la matriz.
VCC RQ ECOSAT
VCC 0.723 . .
RQ 0.581 0.841 .
ECOSAT 0.507 0.679 0.845
FL Criteria table reports square root of AVE on the diagonal and construct correlations on the lower triangle.2.3.3 HTMT
Por último el HTMT es un ratio que si es mayor que 0.90 indica una pérdida de validez discriminante.
VCC RQ ECOSAT
VCC . . .
RQ 0.632 . .
ECOSAT 0.584 0.847 .2.4 Análisis del modelo estructural
Una vez analizados los constructos desde el punto de vista de su composición, debemos analizar el modelo estructural en su conjunto. Partiendo de que el objetivo del PLS es la maximización de la varianza explicada, las medidas más importantes son la fiabilidad, la validez convergente y la validez discriminante del conjunto del modelo.
- R2, coeficiente de determinación y/o % de varianza explicada
- f2 y q2 efecto tamaño
- Q2, relevancia predictiva
2.4.1 Paths
RQ ECOSAT
R^2 0.338 0.461
AdjR^2 0.335 0.459
VCC 0.581 .
RQ . 0.6792.4.2 R2
Buscar R2 mayores de 0.7, aunque valores alrededor de 0.25 sean aceptados según ámbitos; (sustancial mayor que 0.75, moderado alrededor de 0.5 y débil, 0.25). Usar R2adj para comparar modelos con diferente número de constructos y/u observaciones.
RQ ECOSAT
Rsq 0.3377728 0.4611090
AdjRsq 0.3351657 0.45898732.4.3 f2 - effect sizes
El f2 permite evaluar la contribución de cada constructo exógeno a la R2 de un constructo endógeno. Los valores de 0.02, 0.15 y 0.35 indican un efecto pequeño, mediano o grande sobre el constructo endógeno.
VCC RQ ECOSAT
VCC 0.000 0.510 0.000
RQ 0.000 0.000 0.856
ECOSAT 0.000 0.000 0.0002.4.4 Efectos
2.4.4.1 Totales
VCC RQ ECOSAT
VCC 0.000 0.581 0.395
RQ 0.000 0.000 0.679
ECOSAT 0.000 0.000 0.0002.4.4.2 Indirectos
VCC RQ ECOSAT
VCC 0.000 0.000 0.395
RQ 0.000 0.000 0.000
ECOSAT 0.000 0.000 0.0003 Modelización con bootstrapping
Bootstrapping para calcular la significatividad de los paths estimados. Habitualmente se trabaja con un 5% (t > 1.96) lo que implica significatividad al 95%. Podemos cambiar al 10 o al 1 según ámbito. Usar doble bootstrapping si hay menos de 4 constructos.
3.1 Structural paths
Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC -> RQ 0.581 0.587 0.037 15.537 0.506 0.656
RQ -> ECOSAT 0.679 0.682 0.042 16.041 0.600 0.7583.2 Bootstrapped loadings
Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC1 -> VCC 0.794 0.794 0.033 23.972 0.725 0.856
VCC2 -> VCC 0.831 0.829 0.038 21.785 0.744 0.891
VCC3 -> VCC 0.635 0.626 0.063 10.145 0.487 0.729
VCC4 -> VCC 0.865 0.863 0.017 50.086 0.825 0.893
VCC5 -> VCC 0.674 0.668 0.055 12.289 0.547 0.769
VCC6 -> VCC 0.462 0.454 0.079 5.844 0.291 0.590
TRUST -> RQ 0.820 0.820 0.034 24.062 0.741 0.879
COMMIT -> RQ 0.855 0.854 0.024 36.284 0.801 0.896
SOCSAT -> RQ 0.848 0.847 0.021 40.196 0.799 0.883
ECOSAT1 -> ECOSAT 0.934 0.934 0.012 79.886 0.910 0.956
ECOSAT2 -> ECOSAT 0.916 0.917 0.017 52.572 0.879 0.946
ECOSAT3 -> ECOSAT 0.657 0.651 0.057 11.544 0.524 0.747
TRUST1 -> TRUST 0.935 0.934 0.012 79.076 0.909 0.954
TRUST2 -> TRUST 0.832 0.834 0.023 36.609 0.786 0.875
TRUST3 -> TRUST 0.846 0.843 0.032 26.761 0.767 0.893
COMMIT1 -> COMMIT 0.885 0.886 0.016 54.756 0.852 0.915
COMMIT2 -> COMMIT 0.909 0.909 0.013 70.858 0.883 0.932
COMMIT3 -> COMMIT 0.816 0.814 0.036 22.541 0.733 0.875
COMMIT4 -> COMMIT 0.859 0.858 0.029 29.265 0.792 0.906
SOCSAT1 -> SOCSAT 0.769 0.765 0.035 21.709 0.685 0.827
SOCSAT2 -> SOCSAT 0.922 0.922 0.011 86.869 0.901 0.942
SOCSAT3 -> SOCSAT 0.900 0.899 0.016 57.033 0.863 0.9253.3 Bootstrapped HTMT
Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC -> RQ 0.632 0.633 0.048 13.299 0.536 0.720
VCC -> ECOSAT 0.584 0.599 0.042 13.796 0.517 0.682
RQ -> ECOSAT 0.847 0.851 0.057 14.729 0.733 0.9523.4 Total effects (paths)
Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC -> RQ 0.581 0.587 0.037 15.537 0.506 0.656
VCC -> ECOSAT 0.395 0.401 0.042 9.326 0.319 0.482
RQ -> ECOSAT 0.679 0.682 0.042 16.041 0.600 0.7583.5 Plot model
Modelo con bootstrapping
4 Predicción
PLS in-sample metrics:
TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.925 0.814 0.872 1.197 1.166 1.237
MAE 0.707 0.632 0.648 0.949 0.924 0.897
PLS out-of-sample metrics:
TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.932 0.821 0.885 1.207 1.177 1.246
MAE 0.712 0.635 0.658 0.956 0.931 0.903
LM in-sample metrics:
TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.777 0.750 0.654 0.976 0.952 1.053
MAE 0.611 0.568 0.493 0.776 0.744 0.727
LM out-of-sample metrics:
TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.848 0.802 0.717 1.049 1.015 1.121
MAE 0.652 0.601 0.526 0.822 0.787 0.7675 Potencia (pwr)
En nuestro ejemplo tenemos una muestra 256 empresas, y la regresión más complicada es la del constructo con 3 regresores por lo que v=256-3-1=252.
Multiple regression power calculation
u = 3
v = 252
f2 = 0.15
sig.level = 0.05
power = 0.9998353
Multiple regression power calculation
u = 3
v = 72.70583
f2 = 0.15
sig.level = 0.05
power = 0.8El resultado indica que nuestro tamaño muestra posee una potencia igual al valor del resultado de power, ya que el tamaño muestral máximo para una potencia del 80% sería del valor del resultado del valor de v elementos con los parámetros indicados.
En https://forum.smartpls.com/viewtopic.php?f=5&t=3805 hay una “discusión en torno al”greater than 0.9” de Primer PLS … de Hair; lo solventa un investigador / desarrollador de SmartPLS: https://www.researchgate.net/profile/Jan_Michael_Becker↩︎
En nuestro caso al proceder con la eliminación de aquellas cargas menores de 0.7 no mejoraba significativamente el modelo↩︎