NOTA: Incluye constructo de segundo orden

1 Tablas muestra

2 Modelización

El modelo de medida es el siguiente:

Modelo de medida

El modelo estructural es el siguiente:

Modelo estructural

2.1 Análisis de la fiabilidad

Para el modelo de medida se han considerado composites mode A. De este modo, el primer paso debe ser observar el resumen de los indicadores de fiabilidad, consistencia interna y validez.

El resultado del análisis muestra todas las escalas que apoyan las variables latentes tienen un Cronbach’s alpha mayor que 0.7, completado por una fiabilidad del compuesto rhoC también por encima de 0.7. para valores superiores a 0.9¹.

       alpha  rhoC   AVE  rhoA
VCC    0.868 0.900 0.601 0.878
RQ     0.824 0.895 0.739 0.831
ECOSAT 0.825 0.896 0.742 0.836

Alpha, rhoC, and rhoA should exceed 0.7 while AVE should exceed 0.5

2.2 Validez convergente

2.2.1 AVE

Del mismo modo, para evaluar la validez convergente o grado con el que una medida correlaciona positivamente con medidas alternativas del mismo constructo, usamos el coeficiente AVE (average variance extracted) que también cumple con la expectativa de estar por encima de 0.5.

       alpha  rhoC   AVE  rhoA
VCC    0.868 0.900 0.601 0.878
RQ     0.824 0.895 0.739 0.831
ECOSAT 0.825 0.896 0.742 0.836

Alpha, rhoC, and rhoA should exceed 0.7 while AVE should exceed 0.5

Los indicadores son mostrados de forma conjunta en el siguiente gráfico.

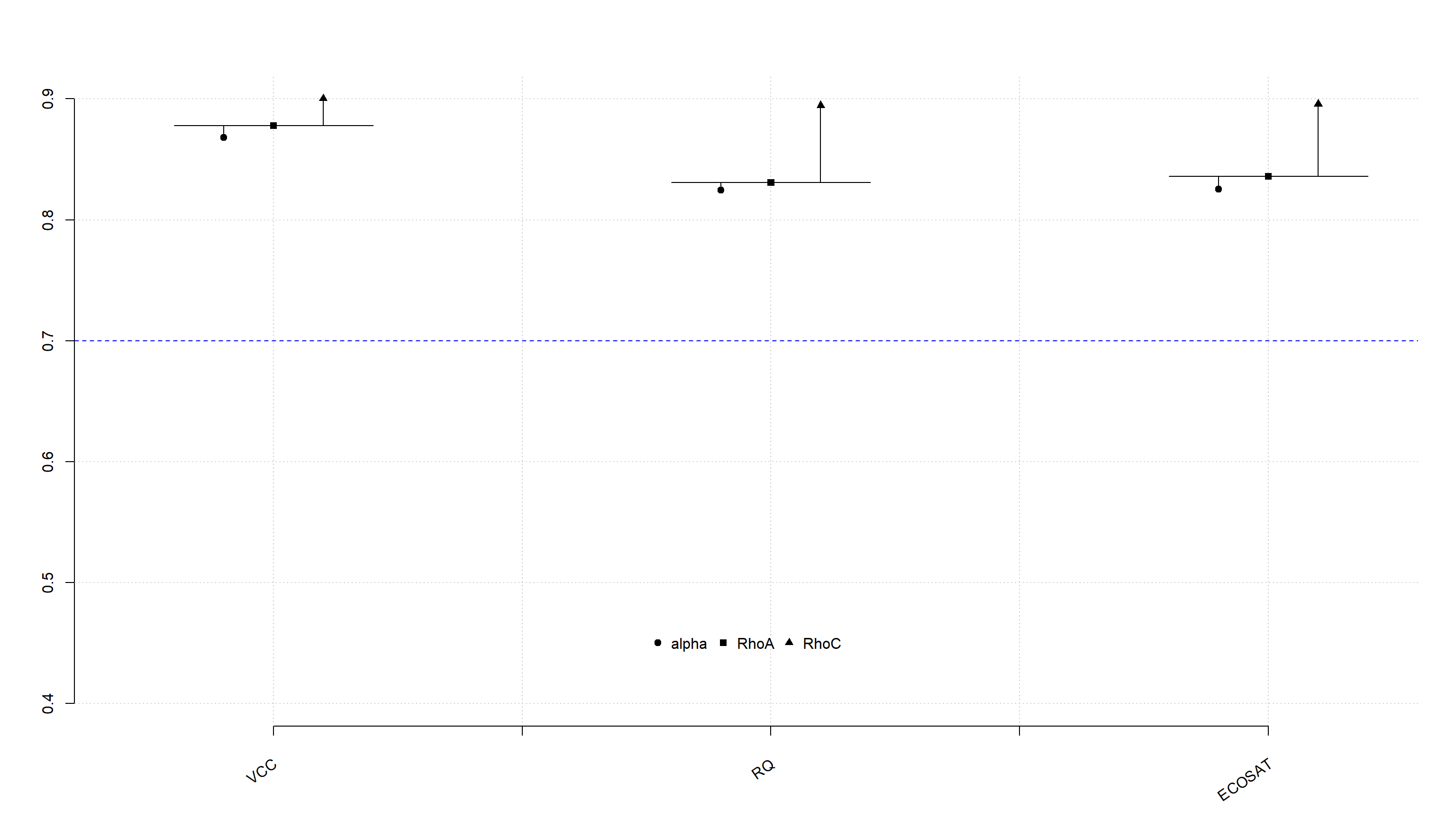
Tabla de fiabilidad

2.2.2 Análisis de las cargas

Por otro lado, es importante analizar también las cargas o loadings, indicadores de la fiabilidad del indicador en el constructo, y que deberían ser mayores de 0.7 para retener el indicador; para aquellas que están entre 0.4 y 0.7 debe ser analizado el comportamiento del constructo ante una eliminación del indicador con carga baja².

          VCC    RQ ECOSAT TRUST COMMIT SOCSAT
VCC1    0.691 0.000  0.000 0.000  0.000  0.000
VCC2    0.774 0.000  0.000 0.000  0.000  0.000
VCC3    0.802 0.000  0.000 0.000  0.000  0.000
VCC4    0.798 0.000  0.000 0.000  0.000  0.000
VCC5    0.806 0.000  0.000 0.000  0.000  0.000
VCC6    0.776 0.000  0.000 0.000  0.000  0.000
TRUST   0.000 0.865  0.000 0.000  0.000  0.000
COMMIT  0.000 0.874  0.000 0.000  0.000  0.000
SOCSAT  0.000 0.839  0.000 0.000  0.000  0.000
ECOSAT1 0.000 0.000  0.861 0.000  0.000  0.000
ECOSAT2 0.000 0.000  0.906 0.000  0.000  0.000
ECOSAT3 0.000 0.000  0.814 0.000  0.000  0.000
TRUST1  0.000 0.000  0.000 0.919  0.000  0.000
TRUST2  0.000 0.000  0.000 0.851  0.000  0.000
TRUST3  0.000 0.000  0.000 0.942  0.000  0.000
COMMIT1 0.000 0.000  0.000 0.000  0.870  0.000
COMMIT2 0.000 0.000  0.000 0.000  0.885  0.000
COMMIT3 0.000 0.000  0.000 0.000  0.813  0.000
COMMIT4 0.000 0.000  0.000 0.000  0.889  0.000
SOCSAT1 0.000 0.000  0.000 0.000  0.000  0.820
SOCSAT2 0.000 0.000  0.000 0.000  0.000  0.932
SOCSAT3 0.000 0.000  0.000 0.000  0.000  0.890

        rowSums(round(summary_simple$loadings, 3))
VCC1                                         0.691
VCC2                                         0.774
VCC3                                         0.802
VCC4                                         0.798
VCC5                                         0.806
VCC6                                         0.776
TRUST                                        0.865
COMMIT                                       0.874
SOCSAT                                       0.839
ECOSAT1                                      0.861
ECOSAT2                                      0.906
ECOSAT3                                      0.814
TRUST1                                       0.919
TRUST2                                       0.851
TRUST3                                       0.942
COMMIT1                                      0.870
COMMIT2                                      0.885
COMMIT3                                      0.813
COMMIT4                                      0.889
SOCSAT1                                      0.820
SOCSAT2                                      0.932
SOCSAT3                                      0.890

2.3 Validez discriminante

2.3.1 Cross-loadings

Para el análisis de la validez discriminante o capacidad de un constructo de ser realmente distinto a otros, utilizamos las denominadas cross-loadings, que miden esa capacidad del constructo. En la tabla adjunta se puede observar en cada indicador carga de forma superior en su variable latente, siendo el resto de cargas de menor intensidad.

          VCC    RQ ECOSAT
VCC1    0.691 0.373  0.301
VCC2    0.774 0.467  0.456
VCC3    0.802 0.426  0.277
VCC4    0.798 0.441  0.382
VCC5    0.806 0.533  0.331
VCC6    0.776 0.591  0.430
TRUST   0.527 0.865  0.514
COMMIT  0.542 0.874  0.612
SOCSAT  0.530 0.839  0.770
ECOSAT1 0.305 0.621  0.861
ECOSAT2 0.469 0.714  0.906
ECOSAT3 0.445 0.592  0.814

2.3.2 Fornell-Larcker

El criterio de Fornell-Larcker, compara la raíz cuadrado del AVE con la correlación de las variables latentes. La raíz cuadrada del AVE de cada constructo, debería ser más grande que la más alta correlación con cualquier otro constructo. Se puede observar en la tabla siguiente que el valor en la diagonal principal, es mayor que el resto de valores en la parte inferior de la matriz.

         VCC    RQ ECOSAT
VCC    0.775     .      .
RQ     0.621 0.860      .
ECOSAT 0.473 0.749  0.861

FL Criteria table reports square root of AVE on the diagonal and construct correlations on the lower triangle.

2.3.3 HTMT

Por último el HTMT es un ratio que si es mayor que 0.90 indica una pérdida de validez discriminante.

         VCC    RQ ECOSAT
VCC        .     .      .
RQ     0.717     .      .
ECOSAT 0.551 0.888      .

2.4 Análisis del modelo estructural

Una vez analizados los constructos desde el punto de vista de su composición, debemos analizar el modelo estructural en su conjunto. Partiendo de que el objetivo del PLS es la maximización de la varianza explicada, las medidas más importantes son la fiabilidad, la validez convergente y la validez discriminante del conjunto del modelo.

R², coeficiente de determinación y/o % de varianza explicada
f² y q² efecto tamaño
Q², relevancia predictiva

2.4.1 Paths

          RQ ECOSAT
R^2    0.385  0.561
AdjR^2 0.383  0.559
VCC    0.621      .
RQ         .  0.749

2.4.2 R²

Buscar R² mayores de 0.7, aunque valores alrededor de 0.25 sean aceptados según ámbitos; (sustancial mayor que 0.75, moderado alrededor de 0.5 y débil, 0.25). Usar R²_adj para comparar modelos con diferente número de constructos y/u observaciones.

              RQ    ECOSAT
Rsq    0.3854870 0.5607058
AdjRsq 0.3831768 0.5590543

2.4.3 f² - effect sizes

El f² permite evaluar la contribución de cada constructo exógeno a la R² de un constructo endógeno. Los valores de 0.02, 0.15 y 0.35 indican un efecto pequeño, mediano o grande sobre el constructo endógeno.

         VCC    RQ ECOSAT
VCC    0.000 0.627  0.000
RQ     0.000 0.000  1.276
ECOSAT 0.000 0.000  0.000

2.4.4 Efectos

2.4.4.1 Totales

         VCC    RQ ECOSAT
VCC    0.000 0.621  0.465
RQ     0.000 0.000  0.749
ECOSAT 0.000 0.000  0.000

2.4.4.2 Indirectos

         VCC    RQ ECOSAT
VCC    0.000 0.000  0.465
RQ     0.000 0.000  0.000
ECOSAT 0.000 0.000  0.000

3 Modelización con bootstrapping

Bootstrapping para calcular la significatividad de los paths estimados. Habitualmente se trabaja con un 5% (t > 1.96) lo que implica significatividad al 95%. Podemos cambiar al 10 o al 1 según ámbito. Usar doble bootstrapping si hay menos de 4 constructos.

3.1 Structural paths

               Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC  ->  RQ            0.621          0.625        0.037  16.746   0.549    0.694
RQ  ->  ECOSAT         0.749          0.751        0.032  23.187   0.684    0.809

3.2 Bootstrapped loadings

                    Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC1  ->  VCC               0.691          0.689        0.044  15.875   0.596    0.765
VCC2  ->  VCC               0.774          0.773        0.039  19.985   0.690    0.841
VCC3  ->  VCC               0.802          0.802        0.028  29.004   0.743    0.851
VCC4  ->  VCC               0.798          0.796        0.028  28.278   0.736    0.846
VCC5  ->  VCC               0.806          0.806        0.029  27.531   0.744    0.858
VCC6  ->  VCC               0.776          0.777        0.025  30.474   0.725    0.822
TRUST  ->  RQ               0.865          0.865        0.022  38.576   0.815    0.903
COMMIT  ->  RQ              0.874          0.875        0.017  50.053   0.838    0.906
SOCSAT  ->  RQ              0.839          0.839        0.023  36.447   0.789    0.880
ECOSAT1  ->  ECOSAT         0.861          0.860        0.032  26.879   0.788    0.912
ECOSAT2  ->  ECOSAT         0.906          0.906        0.015  60.275   0.875    0.932
ECOSAT3  ->  ECOSAT         0.814          0.814        0.028  28.715   0.751    0.864
TRUST1  ->  TRUST           0.919          0.918        0.014  64.539   0.888    0.944
TRUST2  ->  TRUST           0.851          0.850        0.024  34.779   0.798    0.894
TRUST3  ->  TRUST           0.942          0.941        0.010  92.175   0.919    0.959
COMMIT1  ->  COMMIT         0.870          0.871        0.020  43.388   0.827    0.906
COMMIT2  ->  COMMIT         0.885          0.885        0.025  34.824   0.828    0.925
COMMIT3  ->  COMMIT         0.813          0.813        0.038  21.350   0.730    0.878
COMMIT4  ->  COMMIT         0.889          0.889        0.015  60.882   0.859    0.915
SOCSAT1  ->  SOCSAT         0.820          0.818        0.036  22.878   0.740    0.879
SOCSAT2  ->  SOCSAT         0.932          0.932        0.011  81.975   0.908    0.951
SOCSAT3  ->  SOCSAT         0.890          0.890        0.022  41.293   0.841    0.924

3.3 Bootstrapped HTMT

                Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC  ->  RQ             0.717          0.718        0.043  16.494   0.628    0.798
VCC  ->  ECOSAT         0.551          0.551        0.054  10.176   0.439    0.651
RQ  ->  ECOSAT          0.888          0.889        0.037  24.057   0.812    0.956

3.4 Total effects (paths)

                Original Est. Bootstrap Mean Bootstrap SD T Stat. 2.5% CI 97.5% CI
VCC  ->  RQ             0.621          0.625        0.037  16.746   0.549    0.694
VCC  ->  ECOSAT         0.465          0.469        0.034  13.584   0.401    0.534
RQ  ->  ECOSAT          0.749          0.751        0.032  23.187   0.684    0.809

3.5 Plot model

Modelo con bootstrapping

4 Predicción


PLS in-sample metrics:
     TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.847  0.838  0.846   0.865   0.734   1.086
MAE  0.646  0.643  0.628   0.646   0.574   0.799

PLS out-of-sample metrics:
     TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.860  0.849  0.856   0.868   0.740   1.096
MAE  0.653  0.651  0.637   0.649   0.578   0.809

LM in-sample metrics:
     TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.770  0.707  0.570   0.758   0.655   0.966
MAE  0.586  0.549  0.404   0.555   0.483   0.693

LM out-of-sample metrics:
     TRUST COMMIT SOCSAT ECOSAT1 ECOSAT2 ECOSAT3
RMSE 0.819  0.751  0.625   0.812   0.708   1.055
MAE  0.614  0.573  0.437   0.588   0.515   0.736

5 Potencia (pwr)

En nuestro ejemplo tenemos una muestra 268 HOTELES, y la regresión más complicada es la del HCO con 3 regresores por lo que v=268-3-1=264.


     Multiple regression power calculation 

              u = 3
              v = 264
             f2 = 0.15
      sig.level = 0.05
          power = 0.9999052


     Multiple regression power calculation 

              u = 3
              v = 72.70583
             f2 = 0.15
      sig.level = 0.05
          power = 0.8

El resultado indica que nuestro tamaño muestra posee una potencia igual al valor del resultado de power, ya que el tamaño muestral máximo para una potencia del 80% sería del valor del resultado del valor de v elementos con los parámetros indicados.


 matrixpls parameter estimates
                     Est.
VCC~RQ          0.6208760
RQ~ECOSAT       0.7488029
VCC=~VCC1       0.6906674
VCC=~VCC2       0.7739110
VCC=~VCC3       0.8019950
VCC=~VCC4       0.7977945
VCC=~VCC5       0.8057136
VCC=~VCC6       0.7764122
RQ=~TRUST       0.8651128
RQ=~COMMIT      0.8742208
RQ=~SOCSAT      0.8388710
ECOSAT=~ECOSAT1 0.8614340
ECOSAT=~ECOSAT2 0.9059658
ECOSAT=~ECOSAT3 0.8136394

 matrixpls weights
           VCC1      VCC2     VCC3      VCC4     VCC5      VCC6     TRUST    COMMIT    SOCSAT   ECOSAT1   ECOSAT2   ECOSAT3
VCC    0.169696 0.2120515 0.193536 0.2002788 0.242243 0.2685596 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
RQ     0.000000 0.0000000 0.000000 0.0000000 0.000000 0.0000000 0.3437246 0.3840452 0.4373725 0.0000000 0.0000000 0.0000000
ECOSAT 0.000000 0.0000000 0.000000 0.0000000 0.000000 0.0000000 0.0000000 0.0000000 0.0000000 0.3731824 0.4291644 0.3560788

Weight algorithm converged in 4 iterations.

 Total Effects (column on row)
          RQ    ECOSAT
VCC 0.620876 0.4649138
RQ  0.000000 0.7488029

 Direct Effects
          RQ    ECOSAT
VCC 0.620876 0.0000000
RQ  0.000000 0.7488029

 Indirect Effects
    RQ    ECOSAT
VCC  0 0.4649138
RQ   0 0.0000000

 Inner model squared multiple correlations (R2)
      VCC        RQ    ECOSAT 
0.3854870 0.5607058 0.0000000 

 Inner model (composite) residual covariance matrix
          VCC        RQ
VCC 0.6145130 0.2727472
RQ  0.2727472 0.4392942

 Outer model (indicator) residual covariance matrix
             VCC1      VCC2      VCC3      VCC4      VCC5      VCC6     TRUST    COMMIT    SOCSAT   ECOSAT1   ECOSAT2   ECOSAT3
VCC1    0.4770214 0.5345150 0.5539117 0.5510106 0.5564801 0.5362426 0.4116815 0.4229151 0.4121815 0.2330013 0.3474220 0.3287502
VCC2    0.5345150 0.5989382 0.6206727 0.6174219 0.6235506 0.6008739 0.4196019 0.4317504 0.4214270 0.1589651 0.2818976 0.2719201
VCC3    0.5539117 0.6206727 0.6431959 0.6398271 0.6461782 0.6226787 0.4847278 0.4978425 0.4851055 0.3333295 0.4694385 0.4410293
VCC4    0.5510106 0.6174219 0.6398271 0.6364760 0.6427938 0.6194174 0.4674223 0.4803129 0.4682460 0.2393430 0.3699707 0.3515965
VCC5    0.5564801 0.6235506 0.6461782 0.6427938 0.6491744 0.6255659 0.3959559 0.4081732 0.3990963 0.2889090 0.4232729 0.3996585
VCC6    0.5362426 0.6008739 0.6226787 0.6194174 0.6255659 0.6028159 0.3146833 0.3257522 0.3197380 0.1828976 0.3074380 0.2949183
TRUST   0.3302717 0.4117763 0.3768198 0.3896128 0.4695864 0.5193819 0.7484201 0.7562996 0.7257181 0.6523363 0.7388486 0.6213250
COMMIT  0.3268495 0.4083806 0.3727755 0.3857452 0.4664817 0.5170941 0.7562996 0.7642620 0.7333585 0.5789074 0.6621796 0.5520247
SOCSAT  0.3072658 0.3847327 0.3503084 0.3627924 0.4401912 0.4890272 0.7257181 0.7333585 0.7037046 0.3980522 0.4698180 0.3809920
ECOSAT1 0.3303957 0.4723361 0.3208806 0.4114407 0.3683345 0.4504440 0.4637358 0.5489148 0.6841658 0.7420685 0.7804297 0.7008966
ECOSAT2 0.2450998 0.3820387 0.2185910 0.3144552 0.2679468 0.3586441 0.4349188 0.5239454 0.6683452 0.7804297 0.8207739 0.7371294
ECOSAT3 0.2033881 0.3243548 0.1768835 0.2630800 0.2211194 0.3032838 0.4328245 0.5132230 0.6411816 0.7008966 0.7371294 0.6620090

 Residual-based fit indices
                                  Value
Communality                   0.6707383
Redundancy                    0.2194527
SMC                           0.4730964
RMS outer residual covariance 0.4980599
RMS inner residual covariance 0.5042888
SRMR                          0.4581485
SRMR (Henseler)               0.4192245

 Absolute goodness of fit: 0.5633151

 Composite Reliability indices
      VCC        RQ    ECOSAT 
0.9002439 0.8945446 0.8957701 

 Average Variance Extracted indices
      VCC        RQ    ECOSAT 
0.6012703 0.7387956 0.7416172 

 AVE - largest squared correlation
      VCC        RQ    ECOSAT 
0.2157833 0.1780898 0.1809113 

 Heterotrait-monotrait matrix
             VCC        RQ    ECOSAT
VCC    0.0000000 0.0000000 0.0000000
RQ     0.7169120 0.0000000 0.0000000
ECOSAT 0.5507392 0.8877212 0.0000000

 Composite equilevance indices

 CEI individual
      VCC        RQ    ECOSAT 
0.9976680 0.9989866 0.9995095 

 CEI total: 0.997668


 Q2 predictive relevance statistics

 Overall Q2
0.3008463
 Block Q2
      VCC        RQ    ECOSAT 
0.2662846 0.1657157 0.4470999 

 Indicator Q2
       VCC1        VCC2        VCC3        VCC4        VCC5        VCC6     ECOSAT1     ECOSAT2     ECOSAT3       TRUST      COMMIT      SOCSAT 
 0.44630802  0.44893081  0.29914458  0.39027392  0.05668515 -0.06969676  0.41150400  0.62450174  0.27988630 -0.10405813  0.08918320  0.50175853

En https://forum.smartpls.com/viewtopic.php?f=5&t=3805 hay una “discusión en torno al”greater than 0.9” de Primer PLS … de Hair; lo solventa un investigador / desarrollador de SmartPLS: https://www.researchgate.net/profile/Jan_Michael_Becker ↩︎
En nuestro caso al proceder con la eliminación de aquellas cargas menores de 0.7 no mejoraba significativamente el modelo↩︎

PLS - HOTELES

Roberto Gil-Saura

2022-05-10 18:19:51

1 Tablas muestra

2 Modelización

2.1 Análisis de la fiabilidad

2.2 Validez convergente

2.2.1 AVE

2.2.2 Análisis de las cargas

2.3 Validez discriminante

2.3.1 Cross-loadings

2.3.2 Fornell-Larcker

2.3.3 HTMT

2.4 Análisis del modelo estructural

2.4.1 Paths

2.4.2 R²

2.4.3 f² - effect sizes

2.4.4 Efectos

2.4.4.1 Totales

2.4.4.2 Indirectos

3 Modelización con bootstrapping

3.1 Structural paths

3.2 Bootstrapped loadings

3.3 Bootstrapped HTMT

3.4 Total effects (paths)

3.5 Plot model

4 Predicción

5 Potencia (pwr)

PLS - HOTELES

Roberto Gil-Saura

2022-05-10 18:19:51

1 Tablas muestra

2 Modelización

2.1 Análisis de la fiabilidad

2.2 Validez convergente

2.2.1 AVE

2.2.2 Análisis de las cargas

2.3 Validez discriminante

2.3.1 Cross-loadings

2.3.2 Fornell-Larcker

2.3.3 HTMT

2.4 Análisis del modelo estructural

2.4.1 Paths

2.4.2 R2

2.4.3 f2 - effect sizes

2.4.4 Efectos

2.4.4.1 Totales

2.4.4.2 Indirectos

3 Modelización con bootstrapping

3.1 Structural paths

3.2 Bootstrapped loadings

3.3 Bootstrapped HTMT

3.4 Total effects (paths)

3.5 Plot model

4 Predicción

5 Potencia (pwr)

2.4.2 R²

2.4.3 f² - effect sizes